A Virtual Private Network (VPN) connection is an encrypted connection to a server. When you connect to a VPN server and type in a web address, the request is sent via an encrypted signal to the VPN server which then sends you back the web page.
Establishing a VPN connection will keep your ISP or government from recording your browsing history. It can also be used to visit sites that your network administrator has blocked (in some countries like China youtube is blocked). An OpenVPN connection is the most secure type of VPN, because not only is the connection encrypted by
a password, but also by three certificates.
There are many places online that sell VPN services. In this tutorial, I will use vpnbook.com’s service, because it is completely free, and runs entirely off donations.
PART 1: Get A Free OpenVPN Account
Please skip this part if you already have a VPN server set up.
1. Open up your web browser or just click the link to go to www.vpnbook.com.
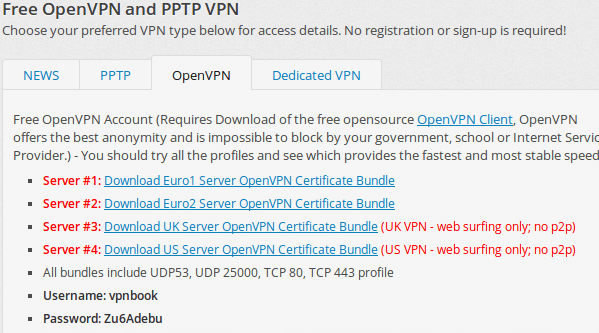
2. Scroll down and click on the tab that says OpenVPN (as the picture shown below). Download one of the certificate bundles and also remember the username and password.
3. Decompress the downloaded package. Create 3 new empty text files in the result folder and called them: ca.crt, certificate.crt, key.key.
4. Open up one of the .ovpn files (All of the .ovpn files are the same, but with different configurations.) with gedit text editor, here I use vpnbook-us1-tcp443.ovpn as example.
5. In the .ovpn file, do following copy and paste things and finally save the changes.
Copy everything between <ca> </ca> tags and paste into ca.crt file.
Copy everything between <cert> </cert> tags and paste into certificate.crt file.
Copy everything between <key> </key> tags and paste into key.key file.
PART 2: Setup OpenVPN connection:
1. Press Ctrl+Alt+T on keyboard to open the terminal. When it opens, run the command below to install VPN plugin for network manager:
sudo apt-get install network-manager-openvpn
2. Go to system area network icon -> VPN Connections -> Configure VPN:
3. Click the Add button in next window and choose OpenVPN in drop-down menu as the connection type.
4. Now in VPN editing window, type in:
Connection name: type a name as you want
Gateway: the IP address in the vpnbook-us1-tcp443.ovpn file.
Type: Password with Certificates (TLS)
Username: see the picture under PART 1 -> step 2.
Password: see the picture under PART 1 -> step 2.
User Certificate: choose the certificate.crt file.
CA Certificate: choose the ca.crt file.
Private Certificate: choose the key.key file.
Private Key Password: leave it empty.
5. NOTE: Advanced settings depend on the .ovpn file you selected in PART 1 (step 4), find the ip, port, cipher and so forth at the top of .ovpn file
Click the Advanced button. Check the boxes which say:
Use custom gateway port: 443
Use LZO data compression
Use a TCP connection
Under Security tab, set Cipher to AES-128-CBC
6. When everything is done, connect to the VPN from network menu:
You’re connected to the VPN if you see this message:
Enjoy!
It’s connected, but no data traffic , no internet connection, I think that I need to set default connection or route vpn one, any ideas bro ?
I have the default route settings except a static ip address added to Address Reservation Table.
You can try connecting the OpenVPN in command line, directly from the profile, and see if it works:
1. Navigate to the result VPNBook.com-* folder:
2. Start the connection with one profile:
Enter the Auth username and password (See pic 1 in the post).
3. In you browser, test the VPN connection.
Thanks for reply, I tried to connect via terminal, it connected but still the same problem, no traffic while connected with the openvpn, traffic come back after disconnect, this is my route table,
Kernel IP routing table
Destination Gateway Genmask Flags Metric Ref Use Iface
default 10.9.2.189 128.0.0.0 UG 0 0 0 tun1
default 192.168.0.1 0.0.0.0 UG 0 0 0 wlan0
10.9.0.1 10.9.2.189 255.255.255.255 UGH 0 0 0 tun1
10.9.2.189 * 255.255.255.255 UH 0 0 0 tun1
93.115.84.195 192.168.0.1 255.255.255.255 UGH 0 0 0 wlan0
128.0.0.0 10.9.2.189 128.0.0.0 UG 0 0 0 tun1
192.168.0.0 * 255.255.255.0 U 9 0 0 wlan0
I know that I have problem with my routes, but tried to fix but failed :D, could you help me plz?
Sorry, I can’t help you about your route settings. But did you try the other OpenVPN servers from vpnbook.com?
Nice tutorial, but:
Keep getting “WARNING: No server certificate verification method has been enabled.” message when trying to connect through terminal by running “openvpn — config vpnbook-us1-tcp443.ovpn”
When using above method, i.e. following all the steps using the GUI exactly, just keeps timing out.
Any suggestions?
I had same problem, I changed permission to these certificate files by chmod -R 700 then attemped again so solved this problem.
” had same problem, I changed permission to these certificate files by chmod -R 700 then attemped again so solved this problem.”
chmod-R 700 ?
Hi, I am new to linux&ubuntu, I am experiencing same problem as mentioned above.Successfull VPN connection message appears but can’t get traffic.
Could you please kindly elaborate your solution/suggestion. Thanks in advance.
Tue Nov 22 12:17:50 2016 ERROR: Cannot ioctl TUNSETIFF tun3: Operation not permitted (errno=1)
Tue Nov 22 12:17:50 2016 Exiting due to fatal error
Worked like a charm.
Thanks
I’have done all the steps as you mentioned but it not connected it is showing me the VPN connection failed help me
I’m using ubuntu 14.04 LTS
theres little problem,,after downloading the OpenVpn file (certificate bundle) i didnt find any .crt and .key file inside the zip file,,so how can i solve it?
thankyou
You make these files up yourself just basic gedit text file and the key you downloaded from the openvpn book server open the file and make 3 text files names as above
5. In the .ovpn file, do following copy and paste things and finally save the changes.
Copy everything between tags and paste into ca.crt file.
Copy everything between tags and paste into certificate.crt file.
Copy everything between tags and paste into key.key file.
I admire you study carefully again, you should yours seprated these files from the main .ovpn file.
Almost everything ok, but there is no internet after establish vpn … any solution ? Cant even ping other side of tunnel.
please read the log file from the /var/log/syslog and find the problem. maybe you don’t set changes in the main .ovpn file to the advance setting such as LZO or TCP or port number.
Just a heads up, in gnome shell type command:
nm-connection-editor
to bring the old interface for the network manager in order to set up the .ovpn config.
Hi, thanks for the tutorial. I need to connect without certificate, only username/password. (SSL connection) did you know how can I do that with this ?
Thanks a lot,
Renan
Hi Thanks for wonderful tutorial. I have a small problem. I want to connect two remote computers using vpnbook. I succesfully setup vpn connection in both computers using same certificate and i got ip in first computer (10.9.0.2) and ip on second (10.9.1.134). Now how can i ping one computer from other. How to complete bridging or routing (whatever necessary) in easy way in ubuntu 14.04? Thanks
I’m running gnome ubuntu 14.04 with openvpn and using vpnbook. I am able to use vpnbook to connect and surf the web and can check that my IP address is successfully changed to the outside.
However, when I try to use any bitTorrent client (e.g. transmission, ktorrent etc.), the client will not start downloading the torrent. It just says it’s stalled or just does nothing. I am using the the certificates and servers (euro 1 or euro 2) which allow p2p sharing. I am able to download torrents with the bitTorrent clients without vpnbook enabled without a problem.
Is there something else I need to do to configure things correctly? …a port change perhaps? There doesn’t seem to be any help for this issue on the internet. And I don’t know if it’s an issue with Ubuntu specifically.
Thanks.
please how do i use the http-proxy-option in the config file?
my mobile provider requires that option.
thanks a lot! but I had to set Google DNS 8.8.4.4
How to configue openvpn through proxy?
Tried :
$ openvpn –config xxx.ovpn –http_proxy servername port proxyauth.txt
It connects to the proxy server the freezes showing :
Initialisation done…(something like that)
Pls help….
Jim,
gut gemacht! Alles in Ordnung!
MfG
Thank you for this tutorial. I was able to install openvpn and set it up bu the openvpn config that I have uses http-proxy-option CUSTOM HEADER. I wonder if you know how I’d be able to get this to work as the base openvpn does not support this option.
The error message I get is:
Options error: Bad http-proxy-option or missing parameter: ‘CUSTOM-HEADER’
I hope someone can help me with this. I would really appreciate it. Thank you.
Hey thanks for the tutorial
i am using Mint 17 and i cant seem to find the OpenVPN from my network setting
first of i created 3 new documents but when i renamed them i wasnt able to open them to add the text that i copied from the opvn files so i added .txt after the new created files for me to be able to edit its content, after i pasted for all 3 files should i delete the .txt from the files or should i leave it as a .txt files
Second thing after installing the openVPN from the terminal by typing the command
sudo apt-get install network-manager-openvpn
i clicked the network setting from the bottom right corner of my task bar to add a VPN connection but i couldnt find OpenVpn from the list, i only found PPTP and an option that says import a saved VPN configaration.
please show me where i am doing wrong
Hey,
Did you ever get this figured out? I am using Mint as well and have no clue whether or not to do this or how to do this…
This should help to get that OpenVPN on the list:
sudo apt-get install network-manager-openvpn-gnome
Help… I’ve followed these directions. I’ve also tried the command line variety with the –config argument. I don’t use Unity, I use GNOME.
I have directly installed openvpn by following command
sudo apt-get install openvpn
and then i tried to access the .opvn file using command
openvpn –config config xxx.ovpn
and the entered the username and password and it diplayed that the
initialisation sequence completed
but the internet is still not working …………
pls help me ..
openvpn needs to run with root privileges, i.e.: sudo openvpn –config xxx.ovpn
I ran into problems with the above guide and solved it as follows. To analyze the problem look (as suggested above) in /var/log/syslog. The reported error here was
Cannot load private key file /…../key.key: error:0B080074:x509 certificate routines:X509_check_private_key:key values mismatch
This means that the the certificate.crt and key.key file do not match. To test this use:
openssl rsa -noout -modulus -in key.key | openssl md5
openssl x509 -noout -modulus -in cert.crt | openssl md5
Both commands should give the same result.
Problem turned out to be caused by line endings (windows/unix) of the key.key file. For some reason gedit decided to convert to unix line endings (although I explicitly saved the file with windows line endings). To test this, use:
cat -v key.key
cat -v cert.crt
In both cases the line endings should look the same on screen and end with ^M (indicating windows style line ending).
In my case the key.key file was the problem. I fixed it using:
unix2dos key.key
After this, everything is working.
I don’t even have Openvpn option in the ‘choose a connection type’ dropdown on 4th picture… Any ideas? Here is output of command ‘sudo apt-get install openvpn’
Reading package lists… Done
Building dependency tree
Reading state information… Done
openvpn is already the newest version.
The following packages were automatically installed and are no longer required:
dbconfig-common gir1.2-gconf-2.0 gir1.2-panelapplet-4.0 gyp
javascript-common kdepimlibs-kio-plugins kdesudo libaccounts-qt1
libakonadi-calendar4 libakonadi-contact4 libakonadi-kabc4 libakonadi-kcal4
libakonadi-kde4 libakonadi-kmime4 libakonadi-notes4 libakonadi-socialutils4
libakonadiprotocolinternals1 libbonobo2-0 libbonobo2-common
libboost-thread1.54.0 libc-ares-dev libc-ares2 libcaca0:i386 libcurl3:i386
libdebconf-kde0 libdevmapper1.02.1:i386 libdmtx0a libgsl0ldbl libgtkspell0
libidl-common libidl0 libidn11:i386 libjs-codemirror libjs-jquery
libjs-jquery-cookie libjs-jquery-event-drag libjs-jquery-metadata
libjs-jquery-mousewheel libjs-jquery-tablesorter libjs-jquery-ui
libjs-node-uuid libjs-underscore libjson0:i386 libkabc4 libkalarmcal2
libkcal4 libkcalcore4 libkcalutils4 libkfbapi1 libkgapi2-2 libkholidays4
libkimap4 libkldap4 libkmbox4 libkmime4 libknewstuff2-4 libkolab0
libkolabxml1 libkpimidentities4 libkpimtextedit4 libkpimutils4
libkprintutils4 libkresources4 libmagick++5 libmailtransport4 libmcrypt4
libmicroblog4 liborbit-2-0 liborbit2 libprison0 libpython2.7:i386
libpython2.7-minimal:i386 libpython2.7-stdlib:i386 libqoauth1 libqrencode3
libreadline6:i386 librtmp0:i386 libsdl1.2debian:i386 libsignon-qt1
libssl-dev libssl-doc libupstart1 libv8-3.14-dev libv8-3.14.5 libxerces-c3.1
libxmu6:i386 linux-image-3.13.0-34-generic
linux-image-extra-3.13.0-34-generic linux-tools-3.13.0-36
linux-tools-3.13.0-36-generic perlmagick python3-pyqt4 python3-sip
zlib1g-dev
Use ‘apt-get autoremove’ to remove them.
0 upgraded, 0 newly installed, 0 to remove and 40 not upgraded.
Hi, i try add my ZPN VPN Profile in my Ubuntu 14.04, but when import the profile i won’t save new config.
I followed everything besides when it says to enter username and password …….. that link did not show those .. id pay for a vpn if it actually fucking worked
I am using Ubuntu 14.04Lts.i did whatever was mentioned above but every time I try to connect,after some time it shows connection failed…plz help…
One more step. In advanced settings check something like “for these resources only. Then – instant connection.
Doesn’t work, and tired countless guides. Does it kill for those who made a VPNGate GUI for windows to make for Ubuntu too?
thanks for the info.. its working…i just followed the guidelines….your great man////
Hi,
I can get vpn connection – tested with ping, but have web problems with both FF and Chrome.
Checked the syslog and get the error :
Dec 31 11:30:31 xxxxxx ntpdate[16335]: Can’t find host 3.ubuntu.pool.ntp.org: Name or service not known (-2)
Dec 31 11:30:31 xxxxx ntpdate[16335]: Can’t find host ntp.ubuntu.com: Name or service not known (-2)
Dec 31 11:30:31 xxxxx ntpdate[16335]: no servers can be used, exiting
Any help will be nice.
Cheers.
Paul
Thanks for the post, but more simplest way (takes 5 minutes) is to use pre-shared key, like described here – `http://sysadm.pp.ua/linux/shifrovanie/openvpn-point-to-point.html . Does anyone used OpenSSL for certs and keys generation for OpenVPN ???
I followed these instructions (thanks– it was fairly easy to do.) and got this message when trying to connect:
the password you use to log in to your computer no longer matches that of your login keyring.
I Googled this message and got a lot of stuff that wasn’t related to VPN, so I tried changing my password in some password application because everyone said it was because it wasn’t my original password (which didn’t work when asked for a password, so not sure if that’s even the issue.) and ultimately got no where fast. so any suggestions would be appreciated. Thanks.
Thanks for the post, however, when I setup the files the key.key file is converted to presentation.
I am using Linux Ubuntu by the way.
Please assist.
thanks for explanation. i want to know that these vpnbook config file is secure or is a trap for data stealing? can you give me your view.
I tired everything as explained but i dont know where i am making mistake. my vpn user show connected in my cybroam firewall. as soon as i connect openvpn (gnome) internet disconnect , and even local resources i am not able to acess. If i select use this connection for network resource in vpn network settings then i could been my lan network but still internet and rdp ,file share etc are not available
i cant find the open vpn option in the select connection option..plz help